Wp/rsk/Квадратна єдначина

Квадратна єдначина у математики то полиномиялна єдначина другого ступню. Имплицитна (обща) форма подполней квадратней єдначине глаши:

$ax^{2}+bx+c=0,\,\!$

з тим же важи же a ≠ 0. (За a = 0, , єдначина постава линеарн.)

Буквиa, b, и c ше наволую коефициєнти: квадратни коефициєнт a то коефициєнт при x², линеарни коефициєнт b то коефициєнт при x, а c шлєбодни член.

Квадратна єдначина вше ма два ришеня.

Ґрафики реалних квадратних функцийох ax² + bx + c. Кажди коефициєнт ше меня окреме.

Квадратна формула

Квадратна єдначина зоз реалнима (або комплекснима) коефициєнтами ма два (нєобовязно розлични ришеня, хтори ше наволую коренї. Ришеня можу будз реални або комплексни, а дати су зоз формулу:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}},$

дзе знак плус-минус ( ± ) означує же и

$x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$

и

$\ x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}$

ришеня датей квадратней єдначини.

Дискриминанта

Приклади розличних знакох дискриминанти
■ <0: x²+¹⁄₂
■ =0: −⁴⁄₃x²+⁴⁄₃x−¹⁄₃
■ >0: ³⁄₂x²+¹⁄₂x−⁴⁄₃

У горнєй формули, подкореньов вираз:

$\Delta =b^{2}-4ac,\,\!$

наволує ше дискриминантa квадратней єдначини.

Квадратна єдначина зоз реалнима коефициєнтами може мац єден або два розлични коренї. У тим случаю, дискриминанта одредзує число и природу кореня. Постоя три случаї:

• Кед дискриминанта позитивна доставаю ше реални и розлични ришеня. При квадратних єдначинох зоз цалочисловима коефициєнтами, кед дискриминанта совершени квадрат, вец коренї рационални числа, а иншак можу будз ирационални числа.
• Кед дискриминанта єднака нули постої лєм єдно ришенє єдначини и воно реалне число. Вон ше наволує и двойнїсти корень, а його вредносц:

  $x=-{\frac {b}{2a}}.\,\!$

• Кед дискриминанта неґативна, ришеня комплексни числа и постоя два розлични комплексни коренї, таки же єден корень комплексни кон’юґат другого.

  ${\begin{aligned}x&={\frac {-b}{2a}}+{\frac {\sqrt {4ac-b^{2}}}{2a}}i,\\x&={\frac {-b}{2a}}-{\frac {\sqrt {4ac-b^{2}}}{2a}}i,\\i^{2}&=-1.\end{aligned}}$

Коренї розлични теди и лєм теди кед дискриминанта розлична од 0, а реални су теди и лєм теди кед дискриминанта нє неґативна.

Ґеометрия

За квадратну функцию:
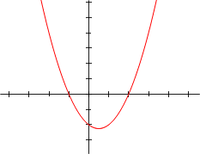
f (x) = x² − x − 2 = (x + 1)(x − 2) реалней пременлївей x, x- координати точки там дзе ґрафик дорушує x-осу, x = −1 и x = 2, то коренї квадратней єдначини: x² − x − 2 = 0.

Коренї квадратней єдначини: $ax^{2}+bx+c=0,\,$ тиж так нули квадратней функциї: $f(x)=ax^{2}+bx+c,\,$ прето же то вредносци x за хтори: $f(x)=0.\,$.

Ако су a, b и c реални числа, и домен функциї f то множество реалних числох, теди нули функциїf точно x-координатиточкох дзе ґрафик дорушує x-осу.

З того шлїдзи же дискриминанта позитивна, ґрафик дотикує х-осу у двох точкох, кед дискриминанта єднака з нулу, теди ґрафик дотикує х-осу у єдней точки, а кед є неґативна вец ґрафик нє дотикує х-осу.

Квадратна факторизация

Вредносц:$x-r,\,$ дзелї полином: $ax^{2}+bx+c,\$

теди и лєм теди кед r корен квадратней єдначини: $ax^{2}+bx+c=0.\$

Зоз квадратней формули шлїдзи же: $ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right).\$

У окремним случаю кед квадратна єдначина нє ма два розлични коренї (т.є. кед дискриминанта єднака з нулу), квадратни полином мож факторовац. $ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.\,\!$

Применьованє на єдначини висшого шора

Oдредзени єдначини висшого шора можу ше ришиц з помоцу квадратних єдначинох. Наприклад: $2x^{6}-3x^{3}+5=0,\,$ може ше записац и як: $2u^{2}-3u+5=0,\$ дзе: $u=x^{3}\$.

Найвекши експонент муши будз два раз векши од експоненту штреднього здаванїка. Тота єдначина ше може ришиц директно аво з хаснованьом єдноставней змени, з помоцу методох за ришованє квадратних єдначинох.

Пообщено, кед полином квадратни за даєдну пременлїву u, дзе $u=x^{n}\,\;$, вец ше квадратна єдначина може хасновац за лєгчейше пренаходзенє ришеня.

История

Вавилонски математичаре знали ришиц задатки у хторих була нєпозната поверхносц або страни правоугелнїка, уж коло 1800. року п. н. е. як цо пренайдзене на глїняних таблїчкох з часу Старого вавилонского царства. Постоя докази на основи хотрих ше тот поступок зявює аж и под час владаня трецей династиї Урох. У сучасней нотациї, задатки, звичайно, подрозумйовали ришованє систему котри творели два єдначини хтори мали форму:$x+y=p,\ \ xy=q$ a еквивалентни су з єдначину: $x^{2}+q=px$.

Вавилонски писаре наводза шлїдуюци крочаї за ришованє спомнутого проблему одредзованя нєпознатих елементох правоугелнїка:

1. Вираховац половку числа p.
2. Квадровац достате число.
3. Одняц q.
4. Одредзиц квадратни корень достатого числа хаснуюци таблїчку квадратох.
5. Поздавац резултати достати у крочайох (1) и (4) же би ше достало х. У сущносци, тот поступок еквивалентни зоз хаснованьом формули

$x={\frac {p}{2}}+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$.

Ґеометрийни методи за ришованє квадратних єдначинох хасновани у Вавилону, Єгипту, Греческей, Китаю и Индиї. Єгипетски папирус хтори походзи зоз часу Штреднього кральовства (од 2050. року п. н. е. до 1650. п. н. е.) нєшка ше чува у Берлину, познати є як Берлински папирус. На папирусу ришовани нєподполни квадратни єдначини хтори маю два члени.

У индийских записох Шулба сутрох, коло 8. вику п. н. е., квадратни єдначини хтори мали форму $ax^{2}=c$ и $ax^{2}+bx=c$ випитовани су хаснуюци ґеометрийни методи.

У Старим Вавилону коло 400. п. н. е. и у Китаю коло 200. п. н. е. почина ше хасновац ґеометрийна метода дисекциї за ришованє квадратних єдначинох зоз позитивнима коренями. Правила за ришованє квадратних єдначинох мож найсц у старокитайским математичним тексту под назву Дзевец кнїжки о математичней схопнoсци. Анї у єдней од тих скорейших ґеометрийних методох хаснованих за одредзованє ришеня квадратней єдначини нєт общей формули.

Гречески математичар Еуклид нашол, коло 300. року п. н. е. , абстрактнєйши ґеометрийни способ за ришованє. Дзекуюци чисто ґеометрийному приступу Питаґора и Еуклид заслужни за пренаходзенє общого способу одредзованя ришеньох квадратней єдначини.

Гречески математичар Диофант ришел квадратну єдначину у своїм дїлу Аритметика, алє представел лєм доставанє єдного ришеня, аж и у задаткох кед обидва коренї позитивни.

Року 628. Брамапутра дал перше експлицитне (алє ище вше нє подполно обще) ришенє квадратней єдначини: $\ ax^{2}+bx=c$, хторе було еквивалентне зоз: $x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}$

Формула за рахованє кореня квадратней єдначини

Способ находзеня формули за пренаходзенє ришеньох квадратней єдначини приказани на шлїдуюцим прикладу:

Дата квадратна єдначина зоз реалнима коефициєнтами $a,b,c\,$:

$ax^{2}+bx+c=0\,$

Тераз цалу єднчину подзелїме зоз першим коефициєнтом $a\,$:

$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\,$

У шлїдуюцим крочаю потребне направиц квадрат биному:

$(x+{\frac {b}{2a}})^{2}-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}}=0\,$

Потим ше познати здаванїки попреруцую на прави бок:

$(x+{\frac {b}{2a}})^{2}={\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\,$

Пошори ше прави бок:

$(x+{\frac {b}{2a}})^{2}={\frac {b^{2}-4ac}{4a^{2}}}\,$

Тераз потребне виражиц $x+{\frac {b}{2a}}\,$:

$x+{\frac {b}{2a}}=\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}\,$

To:

$x+{\frac {b}{2a}}={\frac {\pm {\sqrt {b^{2}-4ac}}}{2a}}\,$

И кед ше преруци ${\frac {b}{2a}}\,$ на прави бок:

$x=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac}}{2a}}\,$

На концу кед ше пошори, достава ше позната формула за вираховйованє кореня квадратней єдначини:

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\,$

У Бакшали рукопису зоз Индиї, хтори походзи з 7. вику була записана алґебeрска формула за ришованє квадратних єдначинох.

Мухамед Ал Хорезми (Персия, 9. вик) розвил множество формулох хтори були добри за ришованє позитивних ришеньох.

Абрахам бар Хия (познати под латинским меном Савасорда) у Европи уведол комплетне ришенє у своєй кнїжки Liber embadorum зоз 12.вику. Баскара 2 (1114. - 1185.) индийски математичар и астроном дал свойо обще ришенє квадратней єдначини за два ришеня.

Списи китайского математичара Янґ Хуия (1238-1298) перши у хторих ше зявюю квадратни єдначини зоз неґативнима коефициєнтами при х, алє вон то приписує Лиу Їу.

Опать ище

• Линеарна єдначина
• Кубна єдначина
• Основна теорема алґебри
• Парабола
• Квадратна функция
• Допуна до подполного квадрату

Литература

• Boyer, Carl Benjamin (1949). The History of the Calculus and its Conceptual Development. Hafner. Dover edition. Template:Wp/rsk/Page
• Courant, Richard. Template:Wp/rsk/Page Introduction to calculus and analysis 1.
• Robert A. Adams. Template:Wp/rsk/Page Calculus: A complete course.
• Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985–1986 Survey, Mathematical Association of America No. 7.
• Cliff Pickover. Template:Wp/rsk/Page Calculus and Pizza: A Math Cookbook for the Hungry Mind.
• Michael Spivak. (September 1994). Template:Wp/rsk/Page Calculus. Publish or Perish publishing.
• Tom M. Apostol. Template:Wp/rsk/Page Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.
• Tom M. Apostol. Template:Wp/rsk/Page Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.
• Silvanus P. Thompson and Martin Gardner. Template:Wp/rsk/Page Calculus Made Easy.
• Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
• Thomas/Finney. Template:Wp/rsk/Page Calculus and Analytic geometry 9th, Addison Wesley.
• Howard Anton, Irl Bivens, Stephen Davis:"Calculus", John Willey and Sons Pte. Ltd. Template:Wp/rsk/Page
• Larson, Ron, Bruce H. Edwards Calculus, , Brooks Cole Cengage Learning. Template:Wp/rsk/Page1
• Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano Calculus, , Addison-Wesley. Template:Wp/rsk/Page1
• Template:Wp/rsk/Cite book
• Crowell, B. (2003). "Calculus". Light and Matter, Fullerton. Приступљено 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdf
• Garrett, P. (2006). "Notes on first year calculus". University of Minnesota. Приступљено 6 May 2007 from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
• Faraz, H. (2006). "Understanding Calculus". Приступљено 6 May 2007 from UnderstandingCalculus.com, URL http://www.understandingcalculus.com (HTML only)
• Keisler, H.J. (2000). "Elementary Calculus: An Approach Using Infinitesimals". Приступљено 29 August 2010 from http://www.math.wisc.edu/~keisler/calc.html
• Mauch, S. (2004). "Sean's Applied Math Book" (pdf). California Institute of Technology. Приступљено 6 May 2007 from https://web.archive.org/web/20070614183657/http://www.cacr.caltech.edu/~sean/applied_math.pdf
• Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Приступљено 6 May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm Template:Wp/rsk/Wayback
• Smith, William V. (2001). "The Calculus". Приступљено 4 July 2008 [1] (HTML only).

Вонкашнї вязи

• Template:Wp/rsk/Springer
• Template:Wp/rsk/MathWorld
• -{101 uses of a quadratic equation Template:Wp/rsk/Wayback}-
• -{101 uses of a quadratic equation: Part II Template:Wp/rsk/Wayback}-