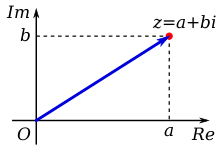
Kompleksno čislo može byti predstavlenym vizualno tako. Kompleksnym čislom v matematikě nazyvaje se čislo , koje se zapisyvaje v formě
a
+
b
i
{\displaystyle a+bi}
a
{\displaystyle a}
pravdiva čest , čislo
b
{\displaystyle b}
izmysljeny koeficijent , a
i
{\displaystyle i}
izmysljenoju jediniceju .
Ktorokoli pravdivo čislo, vozvyšeno v kvadrat, da neodrečny rezultat. Slědovateljno, ravnjenje
x
2
=
−
1
{\displaystyle x^{2}=-1}
x
2
+
1
=
0
{\displaystyle x^{2}+1=0}
±
i
{\displaystyle \pm i}
i
{\displaystyle i}
Kompleksne čisla, pravdiva čest ktoryh jest nulova, nazyvajut se izmysljenymi čislami .
Pravdive čisla sut kompleksne čisla, izmysljena čest ktoryh jest nulova. Slědovateljno, množina pravdivyh čisel jest vlastna podmnožina kompleksnyh čisl.
Čislo
0
{\displaystyle 0}
Vvedenje kompleksnyh čisel jest čestično svezane s rěšenjem kubičnyh ravnjenj. Napravdu, priměnjajuči formulu Cardana k ravnjenju
x
3
−
15
x
−
4
{\displaystyle x^{3}-15x-4}
2
+
11
−
1
3
+
2
−
11
−
1
3
{\displaystyle {\sqrt[{3}]{2+11{\sqrt {-1}}}}+{\sqrt[{3}]{2-11{\sqrt {-1}}}}}
x
3
−
15
x
−
4
{\displaystyle x^{3}-15x-4}
4
{\displaystyle 4}
x
2
+
4
x
+
1
{\displaystyle x^{2}+4x+1}
Dva kompleksne čisla rěče se:
protivpoložene , ako jih pravdive česti sut protivpoložene i jih izmysljene česti tož sut protivpoložene:
−
(
a
+
b
i
)
=
−
a
−
b
i
{\displaystyle -(a+bi)=-a-bi}
sprežene , ako jih pravdive česti sut ravne, a jih izmysljene česti sut protivpoložene:
a
+
b
i
¯
=
a
−
b
i
{\displaystyle {\overline {a+bi}}=a-bi}
Kompleksne čisla često označajut se črez literu
z
{\displaystyle z}
z
=
a
+
b
i
{\displaystyle z=a+bi}
Re
(
z
)
=
a
{\displaystyle {\text{Re}}\left(z\right)=a}
Im
(
z
)
=
b
{\displaystyle {\text{Im}}\left(z\right)=b}
Imajemo:
Re
(
−
z
)
=
−
Re
(
z
)
{\displaystyle {\text{Re}}\left(-z\right)=-{\text{Re}}\left(z\right)}
Im
(
−
z
)
=
−
Im
(
z
)
{\displaystyle {\text{Im}}\left(-z\right)=-{\text{Im}}\left(z\right)}
Re
(
z
¯
)
=
Re
(
z
)
{\displaystyle {\text{Re}}\left({\overline {z}}\right)={\text{Re}}\left(z\right)}
Im
(
z
¯
)
=
−
Im
(
z
)
{\displaystyle {\text{Im}}\left({\overline {z}}\right)=-{\text{Im}}\left(z\right)}
Grafično kompleksne čisla možno prědstaviti v tako zvanoj kompleksnoj ploskosti abo ploskosti Gaussa. Ta ploskost izgledaje, kako koordinatna ploskost, ale osi imajut ine nazvy: pravdiva os (horizontalna) i izmysljena os (vertikalna).
Každomu kompleksnomu čislu odpovědaje ravno jedna točka v ploskosti Gaussa, i každoj točkě v ploskosti Gaussa odpovědaje ravno jedno kompleksno čislo.
Na pravdivoj osi sut pravdive čisla, a na izmysljenoj osi sut izmysljene čisla.
Protivpoložene kompleksne čisla sut surazměrne odnosno početka, a sprežene kompleksne čisla sut surazměrne odnosno pravdivoj osi.
Dekujuči prědstavljeniju kompleksnyh čisel v ploskosti Gaussa, imajemo take dva parametry:
polměr abo modul kompleksnogo čisla jest oddaljenje togo kompleksnogo čisla od početka:
r
=
|
a
+
b
i
|
=
a
2
+
b
2
{\displaystyle r=|a+bi|={\sqrt {a^{2}+b^{2}}}}
argument kompleksnogo čisla jest kut medžu dodatnoj čestju pravdivoj osi i lučem, iže izhodi od početka i prohodi črez to kompleksno čislo. Glavny argument označaje se črez
α
=
Arg
(
a
+
b
i
)
{\displaystyle \alpha ={\text{Arg}}\left(a+bi\right)}
ako
a
=
b
=
0
{\displaystyle a=b=0}
ako
a
=
0
{\displaystyle a=0}
b
>
0
{\displaystyle b>0}
α
=
π
2
{\displaystyle \alpha ={\frac {\pi }{2}}}
ako
a
=
0
{\displaystyle a=0}
b
<
0
{\displaystyle b<0}
α
=
3
2
π
{\displaystyle \alpha ={\frac {3}{2}}\pi }
ako
a
>
0
{\displaystyle a>0}
b
>
0
{\displaystyle b>0}
α
=
arctg
b
a
{\displaystyle \alpha ={\text{arctg}}{\frac {b}{a}}}
ako
a
<
0
{\displaystyle a<0}
α
=
arctg
b
a
+
π
{\displaystyle \alpha ={\text{arctg}}{\frac {b}{a}}+\pi }
ako
a
>
0
{\displaystyle a>0}
b
<
0
{\displaystyle b<0}
α
=
arctg
b
a
+
2
π
{\displaystyle \alpha ={\text{arctg}}{\frac {b}{a}}+2\pi }
Ako kut
α
{\displaystyle \alpha }
α
+
2
k
π
,
π
∈
Z
{\displaystyle \alpha +2k\pi ,\pi \in \mathbb {Z} }
|
−
z
|
=
|
z
|
{\displaystyle |-z|=|z|}
|
z
¯
|
=
|
z
|
{\displaystyle |{\overline {z}}|=|z|}
|
Arg
(
z
)
−
Arg
(
−
z
)
|
=
π
{\displaystyle |{\text{Arg}}\left(z\right)-{\text{Arg}}\left(-z\right)|=\pi }
Arg
(
z
)
+
Arg
(
z
¯
)
=
2
π
{\displaystyle {\text{Arg}}\left(z\right)+{\text{Arg}}\left({\overline {z}}\right)=2\pi }
Forma
a
+
b
i
{\displaystyle a+bi}
algebraična forma kompleksnogo čisla, ale ješče jest dvě formy prědstavjanja kompleksnyh čisl:
trigonometrična forma :
r
(
cos
α
+
i
sin
α
)
{\displaystyle r\left(\cos \alpha +i\sin \alpha \right)}
pokazateljna forma :
r
e
α
i
{\displaystyle re^{\alpha i}}
Imajemo
a
=
r
⋅
cos
α
{\displaystyle a=r\cdot \cos \alpha }
b
=
r
⋅
sin
α
{\displaystyle b=r\cdot \sin \alpha }
Napriměr, možemo napisati
−
1
{\displaystyle -1}
e
π
i
{\displaystyle e^{\pi i}}
e
π
i
=
−
1
{\displaystyle e^{\pi i}=-1}
e
π
i
+
1
=
0
{\displaystyle e^{\pi i}+1=0}
Ta ravnost nazyvvaje se ravnostju Eulera i jest najkrasivějša matematična ravnost. V jej objavjajut se pet najglavnějših čisel:
e
{\displaystyle e}
lim
x
→
+
∞
(
1
+
1
x
)
x
{\displaystyle \lim _{x\rightarrow +\infty }\left(1+{\frac {1}{x}}\right)^{x}}
π
{\displaystyle \pi }
i
{\displaystyle i}
1
{\displaystyle 1}
0
{\displaystyle 0}
Ako imajemo dva kompleksne čisla,
a
+
b
i
{\displaystyle a+bi}
c
+
d
i
{\displaystyle c+di}
(
a
+
b
i
)
+
(
c
+
d
i
)
{\displaystyle \left(a+bi\right)+\left(c+di\right)}
Priměnjajuči svojstva dobavjanija:
(
a
+
b
i
)
+
(
c
+
d
i
)
=
a
+
b
i
+
c
+
d
i
=
a
+
c
+
b
i
+
d
i
=
(
a
+
c
)
+
(
b
+
d
)
i
{\displaystyle \left(a+bi\right)+\left(c+di\right)=a+bi+c+di=a+c+bi+di=\left(a+c\right)+\left(b+d\right)i}
Suma dvoh spreženyh kompleksnyh čisel vsegda jest pravdivo čislo:
(
a
+
b
i
)
+
(
a
−
b
i
)
=
a
+
b
i
+
a
−
b
i
=
2
a
{\displaystyle \left(a+bi\right)+\left(a-bi\right)=a+bi+a-bi=2a}
Da by od odnogo kompleksnogo čisla odjeti drugo, možno do prvogo kompleksnogo čisla dobaviti kompleksne čislo, protivpoložene do drugogo:
(
a
+
b
i
)
−
(
c
+
d
i
)
=
a
+
b
i
−
c
−
d
i
=
a
−
c
+
b
i
−
d
i
=
(
a
−
c
)
+
(
b
−
d
)
i
{\displaystyle \left(a+bi\right)-\left(c+di\right)=a+bi-c-di=a-c+bi-di=\left(a-c\right)+\left(b-d\right)i}
Proizvod dvoh kompleksnyh čisel
a
+
b
i
{\displaystyle a+bi}
c
+
d
i
{\displaystyle c+di}
(
a
+
b
i
)
(
c
+
d
i
)
{\displaystyle \left(a+bi\right)\left(c+di\right)}
(
a
+
b
i
)
(
c
+
d
i
)
=
a
c
+
a
d
i
+
b
c
i
−
b
d
=
a
c
−
b
d
+
a
d
i
+
b
c
i
=
(
a
c
−
b
d
)
+
(
a
d
+
b
c
)
i
{\displaystyle \left(a+bi\right)\left(c+di\right)=ac+adi+bci-bd=ac-bd+adi+bci=\left(ac-bd\right)+\left(ad+bc\right)i}
Proizvod dvoh spreženyh kompleksnyh čisel vsegda jest pravdivo čislo:
(
a
+
b
i
)
(
a
−
b
i
)
=
a
2
+
b
2
{\displaystyle \left(a+bi\right)\left(a-bi\right)=a^{2}+b^{2}}
Pomnožiti dva kompleksne čisla jest prostějše, ako oni sut napisane v pokazateljnoj formě:
r
e
α
i
{\displaystyle re^{\alpha i}}
s
e
β
i
{\displaystyle se^{\beta i}}
r
e
α
i
⋅
s
e
β
i
=
r
s
e
α
i
e
β
i
=
(
r
s
)
e
α
i
+
β
i
=
(
r
s
)
e
(
α
+
β
)
i
{\displaystyle re^{\alpha i}\cdot se^{\beta i}=rse^{\alpha i}e^{\beta i}=\left(rs\right)e^{\alpha i+\beta i}=\left(rs\right)e^{\left(\alpha +\beta \right)i}}
Ako imajemo dva kompleksne čisla,
a
+
b
i
{\displaystyle a+bi}
c
+
d
i
≠
0
{\displaystyle c+di\neq 0}
a
+
b
i
c
+
d
i
{\displaystyle {\frac {a+bi}{c+di}}}
c
−
d
i
{\displaystyle c-di}
a
+
b
i
c
+
d
i
=
(
a
+
b
i
)
(
c
−
d
i
)
(
c
+
d
i
)
(
c
−
d
i
)
=
a
c
−
a
d
i
+
b
c
i
+
b
d
c
2
+
d
2
=
a
c
+
b
d
c
2
+
d
2
+
b
c
−
a
d
c
2
+
d
2
i
{\displaystyle {\frac {a+bi}{c+di}}={\frac {\left(a+bi\right)\left(c-di\right)}{\left(c+di\right)\left(c-di\right)}}={\frac {ac-adi+bci+bd}{c^{2}+d^{2}}}={\frac {ac+bd}{c^{2}+d^{2}}}+{\frac {bc-ad}{c^{2}+d^{2}}}i}
Poděliti odno kompleksno čislo na drugo, odzlične od nuly, jest prostějše, ako oni sut napisane v pokazateljnoj formě. Togda imajemo:
r
e
α
i
s
e
β
i
=
r
s
e
α
i
e
β
i
=
r
s
e
α
i
−
β
i
=
r
s
e
(
α
−
β
)
i
{\displaystyle {\frac {re^{\alpha i}}{se^{\beta i}}}={\frac {r}{s}}{\frac {e^{\alpha i}}{e^{\beta i}}}={\frac {r}{s}}e^{\alpha i-\beta i}={\frac {r}{s}}e^{\left(\alpha -\beta \right)i}}
Ako pokazatelj jest cěl, vozvysiti kompleksne čislo v močnost togo pokazatelja jest najprostějše, ako ono jest napisano v pokazateljnoj formě:
(
r
e
α
i
)
n
=
r
n
e
n
i
α
,
n
∈
Z
{\displaystyle \left(re^{\alpha i}\right)^{n}=r^{n}e^{ni^{\alpha }},n\in \mathbb {Z} }
Vozvysiti jedno kompleksno čislo do močnosti drugogo kompleksnogo čisla jest najprostějše, ako osnova jest napisana v pokazateljnoj formě, a pokazatelj v algebraičnoj:
(
r
e
α
i
)
c
+
d
i
=
(
r
e
α
i
)
c
(
r
e
α
i
)
d
i
=
r
c
e
c
α
i
r
d
i
e
−
d
α
=
r
c
e
d
α
e
c
α
i
(
r
d
)
i
=
r
c
e
d
α
e
c
α
i
e
ln
(
r
d
)
i
=
r
c
e
d
α
e
c
α
i
e
i
ln
r
d
=
r
c
e
d
α
e
(
c
α
+
d
ln
r
)
i
.
{\displaystyle \left(re^{\alpha i}\right)^{c+di}=\left(re^{\alpha i}\right)^{c}\left(re^{\alpha i}\right)^{di}=r^{c}e^{c\alpha i}r^{di}e^{-d\alpha }={\frac {r^{c}}{e^{d\alpha }}}e^{c\alpha i}\left(r^{d}\right)^{i}={\frac {r^{c}}{e^{d\alpha }}}e^{c\alpha i}e^{\ln \left(r^{d}\right)^{i}}={\frac {r^{c}}{e^{d\alpha }}}e^{c\alpha i}e^{i\ln r^{d}}={\frac {r^{c}}{e^{d\alpha }}}e^{\left(c\alpha +d\ln r\right)i}.}
Iztrgnuti korenj iz kompleksnogo čisla jest najprostějše, ako ono jest napisano v pokazateljnoj formě. Dlja togo koristi se tako zvana formula De Moivre’a :
r
e
α
i
n
=
r
n
e
α
i
n
=
r
n
e
α
+
2
k
π
n
i
,
n
∈
N
,
k
=
0
,
1
,
2...
,
n
.
{\displaystyle {\sqrt[{n}]{re^{\alpha i}}}={\sqrt[{n}]{r}}{\sqrt[{n}]{e^{\alpha i}}}={\sqrt[{n}]{r}}e^{{\frac {\alpha +2k\pi }{n}}i},n\in \mathbb {N} ,k=0,1,2...,n.}
Ako
k
=
0
{\displaystyle k=0}
glavny korenj :
r
n
e
α
n
i
{\displaystyle {\sqrt[{n}]{r}}e^{\alpha }{n}i}
Izčisliti prirodny logaritm iz kompleksnogo čisla, odzličnogo od nuly, jest najprostějše, ako ono jest napisano v pokazateljnoj formě:
ln
(
r
e
α
i
)
=
ln
r
+
ln
e
α
i
=
ln
r
+
(
α
+
2
n
π
)
i
,
r
≠
0
,
n
∈
Z
{\displaystyle \ln \left(re^{\alpha i}\right)=\ln r+\ln e^{\alpha i}=\ln r+\left(\alpha +2n\pi \right)i,r\neq 0,n\in \mathbb {Z} }
Ako
n
=
0
{\displaystyle n=0}
glavny prirodny logaritm :
ln
r
+
α
i
{\displaystyle \ln r+\alpha i}
Ako osnova i argument logaritma sut dva kompleksne čisla, odzlične od nuly (prvo takože jest odzlične od jedinice) i napisane v pokazateljnoj formě, togda imajemo tako:
log
r
e
α
i
(
s
e
β
i
)
=
ln
(
s
e
β
i
)
ln
(
r
e
α
i
)
=
ln
s
+
(
β
+
2
m
π
)
i
ln
r
+
(
α
+
2
n
π
)
i
,
r
e
α
i
≠
1
,
r
,
s
≠
0
{\displaystyle \log _{re^{\alpha i}}\left(se^{\beta i}\right)={\frac {\ln \left(se^{\beta i}\right)}{\ln \left(re^{\alpha i}\right)}}={\frac {\ln s+\left(\beta +2m\pi \right)i}{\ln r+\left(\alpha +2n\pi \right)i}},re^{\alpha i}\neq 1,r,s\neq 0}
Ako
m
=
n
=
0
{\displaystyle m=n=0}
glavny logaritm :
ln
s
+
β
i
ln
r
+
α
i
{\displaystyle {\frac {\ln s+\beta i}{\ln r+\alpha i}}}
Uže znajemo, že
cos
α
+
i
sin
α
=
e
α
i
{\displaystyle \cos \alpha +i\sin \alpha =e^{\alpha i}}
Zaměnimo
α
{\displaystyle \alpha }
−
α
{\displaystyle -\alpha }
cos
α
−
i
sin
α
=
e
−
α
i
{\displaystyle \cos \alpha -i\sin \alpha =e^{-\alpha i}}
Odimajuči od prvoj ravnosti vtoru, imajemo:
2
i
sin
α
=
e
α
i
−
e
−
α
i
{\displaystyle 2i\sin \alpha =e^{\alpha i}-e^{-\alpha i}}
sin
α
=
e
α
i
−
e
−
α
i
2
i
{\displaystyle \sin \alpha ={\frac {e^{\alpha i}-e^{-\alpha i}}{2i}}}
Dobavjajuči do prvoj ravnosti vtoru, imajemo:
2
cos
α
=
e
α
i
+
e
−
α
i
{\displaystyle 2\cos \alpha =e^{\alpha i}+e^{-\alpha i}}
cos
α
=
e
α
i
+
e
−
α
i
2
{\displaystyle \cos \alpha ={\frac {e^{\alpha i}+e^{-\alpha i}}{2}}}
Koristajuči te dvě totožnosti, možemo nadjti trigonometrične funkcije kompleksnyh čisel (kompleksne čisla budut napisane v algebraičnoj formě).
Sinus kompleksnogo čisla nahodi se tako:
sin
(
a
+
b
i
)
=
sin
a
cos
b
i
+
cos
a
sin
b
i
=
sin
a
e
−
b
+
e
b
2
+
cos
a
e
−
b
−
e
b
2
i
=
sin
a
cosh
b
+
i
cos
a
sinh
b
{\displaystyle \sin \left(a+bi\right)=\sin a\cos bi+\cos a\sin bi=\sin a{\frac {e^{-b}+e^{b}}{2}}+\cos a{\frac {e^{-b}-e^{b}}{2i}}=\sin a\cosh b+i\cos a\sinh b}
Kosinus kompleksnogo čisla jest:
cos
(
a
+
b
i
)
=
cos
a
cos
b
i
−
sin
a
sin
b
i
=
cos
a
e
−
b
+
e
b
2
−
sin
a
e
−
b
−
e
b
2
i
=
cos
a
cosh
b
−
i
sin
a
sinh
b
{\displaystyle \cos \left(a+bi\right)=\cos a\cos bi-\sin a\sin bi=\cos a{\frac {e^{-b}+e^{b}}{2}}-\sin a{\frac {e^{-b}-e^{b}}{2i}}=\cos a\cosh b-i\sin a\sinh b}
Tangensom nazyvaje se odnošenje medžu sinusom i kosinusom:
tg
(
a
+
b
i
)
=
sin
a
cosh
b
+
i
cos
a
sinh
b
cos
a
cosh
b
−
i
sin
a
sinh
b
,
a
+
b
i
≠
π
2
+
n
π
=
{\displaystyle {\text{tg}}\left(a+bi\right)={\frac {\sin a\cosh b+i\cos a\sinh b}{\cos a\cosh b-i\sin a\sinh b}},a+bi\neq {\frac {\pi }{2}}+n\pi =}
Děleči čiseljnik i imenovnik na
cos
a
cosh
b
{\displaystyle \cos a\cosh b}
Failed to parse (unknown function "\space"): {\displaystyle =\frac{\text{tg}\space a+i\tanh b}{1-i\space\text{tg}\space a\tanh b}=\frac{\left(\text{tg}\space a+i\tanh b\right)\left(1+i\space\text{tg}\space a\tanh b\right)}{\left(1-i\space\text{tg}\space a\tanh b\right)\left(1+i\space\text{tg}\space a\tanh b\right)}=\frac{\text{tg}\space a+i\space\text{tg}^2 a\tanh b+i\tanh b-\text{tg}\space a\tanh^2 b}{\text{tg}^2 a\tanh^2 b+1}=\frac{\text{tg}\left(1-\tanh^2 b\right)}{\text{tg}^2 a\tanh^2 b+1}+\frac{\tanh b\left(\text{tg}^2 a+1\right)}{\text{tg}^2 a\tanh^2 b+1}i=}
Failed to parse (unknown function "\space"): {\displaystyle =\frac{\text{tg}\space\text{sech}^2 b}{\text{tg}^2 a\tanh^2 b+1}+\frac{\tanh b\sec^2 a}{\text{tg}^2 a\tanh^2 b+1},a+bi\ne\frac{\pi}{2}+n\pi,n\in\mathbb{Z}}
Kotangensom nazyaje se odnošenje medžu kosinusom i sinusom:
ctg
(
a
+
b
i
)
=
cos
a
cosh
b
−
i
sin
a
sinh
b
sin
a
cosh
b
+
i
cos
a
sinh
b
=
{\displaystyle {\text{ctg}}\left(a+bi\right)={\frac {\cos a\cosh b-i\sin a\sinh b}{\sin a\cosh b+i\cos a\sinh b}}=}
Děleči čiseljnik i imenovnik na
sin
a
sinh
b
{\displaystyle \sin a\sinh b}
Failed to parse (unknown function "\space"): {\displaystyle =\frac{\text{ctg}\space a\coth b-i}{\coth b+i\space\text{ctg}\space a}=\frac{\left(\text{ctg}\space a\coth b-i\right)\left(\coth b-i\space\text{ctg}\space a\right)}{\left(\coth b+i\space\text{ctg}\space a\right)\left(\coth b-i\space\text{ctg}\space a\right)}=\frac{\text{ctg}\space a\coth^2 b-i\space\text{ctg}^2 a\coth b-i\coth b-\text{ctg}^2 a}{\coth^2 b+\text{ctg}^2 a}=\frac{\text{ctg}\space a\left(\coth^2 b-\text{ctg}\space a\right)}{\coth^2 b+\text{ctg}^2 a}-\frac{\coth b\left(\text{ctg}^2 a+1\right)}{\coth^2 b+\text{ctg}^2 a}i=}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/incubator.wikimedia.org/v1/":): {\displaystyle =\frac{\text{ctg}\space a\left(\coth^2 b-\text{ctg}\space a\right)}{\coth^2 b+\text{ctg}^2 a}-\frac{\coth b\csc^2 a}{\coth^2 b+\text{ctg}^2 a}i,a+bi\ne n\pi, n\in\mathbb{Z}}
Sekansom nazyvaje se čislo, obratno kosinusu:
sec
(
a
+
b
i
)
=
1
cos
a
cosh
b
−
i
sin
a
sinh
b
=
cos
a
cosh
b
+
i
sin
a
sinh
b
cos
2
a
cosh
2
b
+
sin
2
a
sinh
2
b
=
cos
a
cosh
b
sin
2
a
sinh
2
b
+
cos
2
a
cosh
2
b
+
sin
a
sinh
b
sin
2
a
sinh
2
b
+
cos
2
a
cosh
2
b
i
=
{\displaystyle \sec \left(a+bi\right)={\frac {1}{\cos a\cosh b-i\sin a\sinh b}}={\frac {\cos a\cosh b+i\sin a\sinh b}{\cos ^{2}a\cosh ^{2}b+\sin ^{2}a\sinh ^{2}b}}={\frac {\cos a\cosh b}{\sin ^{2}a\sinh ^{2}b+\cos ^{2}a\cosh ^{2}b}}+{\frac {\sin a\sinh b}{\sin ^{2}a\sinh ^{2}b+\cos ^{2}a\cosh ^{2}b}}i=}
Děleči čiseljnik i imenovnik prvogo ulomka na
cos
2
a
cosh
2
b
{\displaystyle \cos ^{2}a\cosh ^{2}b}
sin
2
a
sinh
2
b
{\displaystyle \sin ^{2}a\sinh ^{2}b}
Failed to parse (unknown function "\space"): {\displaystyle =\frac{\sec a\space\text{sech}\space b}{\text{tg}^2 a\tanh^2 b+1}+\frac{\csc a\space\text{csch}\space b}{\text{ctg}^2 a\coth^2 b+1}i,a+bi\ne\frac{\pi}{2}+n\pi, n\in\mathbb{Z}.}
Kosekansom nazyvaje se čislo, obratno sinusu:
csc
(
a
+
b
i
)
=
1
sin
a
cosh
b
+
i
cos
a
sinh
b
=
sin
a
cosh
b
−
i
cos
a
sinh
b
sin
2
a
cosh
2
b
+
cos
2
a
sinh
2
b
=
sin
a
cosh
b
sin
2
a
cosh
2
b
+
cos
2
a
sinh
2
b
−
cos
a
sinh
b
sin
2
a
cosh
2
b
+
cos
2
a
sinh
2
b
i
=
{\displaystyle \csc \left(a+bi\right)={\frac {1}{\sin a\cosh b+i\cos a\sinh b}}={\frac {\sin a\cosh b-i\cos a\sinh b}{\sin ^{2}a\cosh ^{2}b+\cos ^{2}a\sinh ^{2}b}}={\frac {\sin a\cosh b}{\sin ^{2}a\cosh ^{2}b+\cos ^{2}a\sinh ^{2}b}}-{\frac {\cos a\sinh b}{\sin ^{2}a\cosh ^{2}b+\cos ^{2}a\sinh ^{2}b}}i=}
Děleči čiseljnik i imenovnik prvogo ulomka na
sin
2
a
cosh
2
b
{\displaystyle \sin ^{2}a\cosh ^{2}b}
cos
2
a
sinh
2
b
{\displaystyle \cos ^{2}a\sinh ^{2}b}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/incubator.wikimedia.org/v1/":): {\displaystyle =\frac{\csc a\space\text{sech}\space b}{\text{ctg}^2 a\tanh^2 b+1}-\frac{\sec a\space\text{csch}\space b}{\text{tg}^2 a\coth^2 b+1}i,a+bi\ne n\pi, n\in\mathbb{Z}.}
Obratne trigonometrične funckije takože sut oprěděljene dlja kompleksnyh čisl, ale koristajut se malo. Zaměsto togo, se rěšajut trigonometrične ravnjanja, napriměr:
cos
z
=
a
{\displaystyle \cos z=a}
e
z
i
+
e
−
z
i
2
=
a
{\displaystyle {\frac {e^{zi}+e^{-zi}}{2}}=a}
e
z
i
+
e
−
z
i
=
2
a
{\displaystyle e^{zi}+e^{-zi}=2a}
Zaměnjajuči
e
z
i
=
t
{\displaystyle e^{zi}=t}
t
+
1
t
=
2
a
{\displaystyle t+{\frac {1}{t}}=2a}
t
2
+
1
=
2
a
t
{\displaystyle t^{2}+1=2at}
t
2
−
2
a
t
+
1
=
0
{\displaystyle t^{2}-2at+1=0}
D
4
=
a
2
−
1
=
(
a
−
1
)
(
a
+
1
)
{\displaystyle {\frac {D}{4}}=a^{2}-1=\left(a-1\right)\left(a+1\right)}
t
=
a
±
(
a
−
1
)
(
a
+
1
)
{\displaystyle t=a\pm {\sqrt {\left(a-1\right)\left(a+1\right)}}}
Togda:
e
z
i
=
a
±
(
a
−
1
)
(
a
+
1
)
{\displaystyle e^{zi}=a\pm {\sqrt {\left(a-1\right)\left(a+1\right)}}}
z
i
=
ln
(
a
±
(
a
−
1
)
(
a
+
1
)
)
{\displaystyle zi=\ln \left(a\pm {\sqrt {\left(a-1\right)\left(a+1\right)}}\right)}
z
=
2
n
π
−
i
ln
(
a
±
(
a
−
1
)
(
a
+
1
)
)
,
n
∈
Z
{\displaystyle z=2n\pi -i\ln \left(a\pm {\sqrt {\left(a-1\right)\left(a+1\right)}}\right),n\in \mathbb {Z} }










![{\displaystyle {\sqrt[{3}]{2+11{\sqrt {-1}}}}+{\sqrt[{3}]{2-11{\sqrt {-1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a7715f6c438c6123a9866c6fe0ce9f670cf7def)




























































![{\displaystyle {\sqrt[{n}]{re^{\alpha i}}}={\sqrt[{n}]{r}}{\sqrt[{n}]{e^{\alpha i}}}={\sqrt[{n}]{r}}e^{{\frac {\alpha +2k\pi }{n}}i},n\in \mathbb {N} ,k=0,1,2...,n.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a873ecc5d091d4579bc6b93d6591833f5c8b63)

![{\displaystyle {\sqrt[{n}]{r}}e^{\alpha }{n}i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e3e92c3352bd7a20e7ebb7c97dbe7071ce61b79)




































